。
Defn(高斯测度): 对于一个集合 S ⊆ R n S\subseteq \mathbb R^n S ⊆ R n
γ n ( S ) ≜ ∫ S ( 1 2 π ) n exp ( − 1 2 ∥ x ∥ 2 2 ) \gamma_n(S)\triangleq \int_S \left( \dfrac 1{\sqrt{2\pi}} \right)^n \exp\left(-\dfrac 12 \|x\|_2^2\right)
γ n ( S ) ≜ ∫ S ( 2 π 1 ) n exp ( − 2 1 ∥ x ∥ 2 2 )
Thm: α > 0 \alpha>0 α > 0 α \alpha α ϵ > 0 , δ > 0 \epsilon>0,\delta>0 ϵ > 0 , δ > 0
设 K ⊆ R n K\subseteq \mathbb R^n K ⊆ R n x ∈ K ⟺ − x ∈ K x\in K\Longleftrightarrow -x\in K x ∈ K ⟺ − x ∈ K γ n ( K ) ≥ e − α n \gamma_n(K)\ge \text e^{-\alpha n} γ n ( K ) ≥ e − α n x ∈ K ∩ [ − ϵ , ϵ ] n x\in K\cap [-\epsilon,\epsilon]^n x ∈ K ∩ [ − ϵ , ϵ ] n
# { i ∈ [ n ] ∣ x i ∈ { − ϵ , ϵ } } ≥ δ n \#\{ i\in [n]\mid x_i\in\{-\epsilon,\epsilon\} \}\ge \delta n
# { i ∈ [ n ] ∣ x i ∈ { − ϵ , ϵ } } ≥ δ n
并且该算法的错误概率至多为 e Θ ϵ , δ ( n ) \text e^{\Theta_{\epsilon,\delta}(n)} e Θ ϵ , δ ( n )
算法具体执行过程如下:
随机一个向量 x 0 ∼ N ( 0 , I n ) x_0\sim \mathcal N(0,I_n) x 0 ∼ N ( 0 , I n )
求解这样一个优化问题:x = argmin { ∥ x − x 0 ∥ 2 ∣ x ∈ K ∩ [ − ϵ , ϵ ] n } x=\text{argmin}\{\|x-x_0\|_2 \mid x\in K\cap [-\epsilon,\epsilon]^n\} x = argmin { ∥ x − x 0 ∥ 2 ∣ x ∈ K ∩ [ − ϵ , ϵ ] n }
输出 x x x
我们不加证明的使用如下几个引理:
Lemma 1: 若 f : R n → R f:\mathbb R^n\to \mathbb R f : R n → R L L L
Pr x ∼ N ( 0 , I n ) [ ∣ f ( x ) − E [ f ( x ) ] ∣ > L t ] ≤ e − t 2 / 2 \Pr_{x\sim \mathcal N(0,I_n)}[|f(x)-\mathbb E[f(x)]|> Lt]\le\text e^{-t^2/2}
x ∼ N ( 0 , I n ) Pr [ ∣ f ( x ) − E [ f ( x ) ] ∣ > L t ] ≤ e − t 2 / 2
Lemma 2(Šidak-Kathri Formula): 设 K ⊆ R n K\subseteq \mathbb R^n K ⊆ R n S S S a a a S = { x ∈ R n ∣ ∣ ⟨ a , x ⟩ ∣ < 1 } S=\{x\in \mathbb R^n\mid |\langle a,x\rangle|<1\} S = { x ∈ R n ∣ ∣ ⟨ a , x ⟩ ∣ < 1 } γ n ( K ∩ S ) ≥ γ n ( K ) ⋅ γ n ( S ) \gamma_n(K ∩S) ≥ γ_n(K )·γ_n(S) γ n ( K ∩ S ) ≥ γ n ( K ) ⋅ γ n ( S )
Lemma 3(Gaussian Variant of Urysohn’s Inequality): 设 K ⊆ R n K\subseteq \mathbb R^n K ⊆ R n r > 0 r>0 r > 0 γ n ( K ) = γ n ( r B 2 n ) \gamma_n(K)=\gamma_n(rB_2^n) γ n ( K ) = γ n ( r B 2 n ) w ( K ) ≥ w ( r B 2 n ) = r w(K)\ge w(rB_2^n)=r w ( K ) ≥ w ( r B 2 n ) = r
w ( K ) = E g ∼ N ( 0 , I n ) [ max x ∈ K ⟨ g , x ⟩ ] w(K)=\mathop{\mathbb E}\limits_{g\sim \mathcal N(0,I_n)}\left[\max_{x\in K}\langle g,x \rangle\right]
w ( K ) = g ∼ N ( 0 , I n ) E [ x ∈ K max ⟨ g , x ⟩ ]
Lemma 4: 设 K ⊆ R n K\subseteq \mathbb R^n K ⊆ R n γ n ( K ) ≥ e − α n ( α > 0 ) \gamma_n(K)\ge \text e^{-\alpha n}\ (\alpha>0) γ n ( K ) ≥ e − α n ( α > 0 ) w ( K ) ≥ 1 2 e − α n w(K)\ge\dfrac 12 \text e^{-\alpha}\sqrt n w ( K ) ≥ 2 1 e − α n
Proof: 设 r > 0 r>0 r > 0 γ n ( K ) = γ n ( r B 2 n ) \gamma_n(K)=\gamma_n(rB_2^n) γ n ( K ) = γ n ( r B 2 n ) w ( K ) ≥ r w(K)\ge r w ( K ) ≥ r r r r
又由基本事实 2 n ≤ Vol n ( n B 2 n ) ≤ 5 n ( n ≥ 1 ) 2^n\le \text{Vol}_n(\sqrt n B_2^n)\le 5^n\ (n\ge 1) 2 n ≤ Vol n ( n B 2 n ) ≤ 5 n ( n ≥ 1 ) Vol n ( Q ) \text{Vol}_n(Q) Vol n ( Q ) Q Q Q 0 0 0 γ n ( 0 ) = ( 1 2 π ) n \gamma_n(0)=\left(\dfrac 1{\sqrt{2\pi}}\right)^n γ n ( 0 ) = ( 2 π 1 ) n
γ n ( n 2 e α B 2 n ) ≤ Vol n ( n 2 e α B 2 n ) ⋅ γ n ( 0 ) ≤ ( 5 2 e α ) n ( 1 2 π ) n ≤ e − α n \gamma_n\left(\dfrac{\sqrt n}{2\text e^\alpha}B_2^n\right)\le \text{Vol}_n\left(\dfrac{\sqrt n}{2\text e^\alpha}B_2^n\right)\cdot \gamma_n(0)\le \left(\dfrac 5{2\text e^\alpha}\right)^n\left(\dfrac 1{\sqrt{2\pi}}\right)^n\le \text e^{-\alpha n}
γ n ( 2 e α n B 2 n ) ≤ Vol n ( 2 e α n B 2 n ) ⋅ γ n ( 0 ) ≤ ( 2 e α 5 ) n ( 2 π 1 ) n ≤ e − α n
故 r ≥ n 2 e α r\ge \dfrac{\sqrt n}{2\text e^\alpha} r ≥ 2 e α n □ \Box □
Lemma 5: 设 K ⊆ R n K\subseteq \mathbb R^n K ⊆ R n γ n ( K ) ≥ e − α n ( α ≥ 1 ) \gamma_n(K)\ge \text e^{-\alpha n}\ (\alpha\ge 1) γ n ( K ) ≥ e − α n ( α ≥ 1 ) n n n
E x ∼ N ( 0 , I n ) [ d ( x , K ) ] ≤ n ( 1 − 1 512 α e 4 α ) \mathop{\mathbb E}\limits_{x\sim \mathcal N(0,I_n)}[d(x,K)]\le \sqrt n\left(1-\dfrac 1{512\alpha \text e^{4\alpha}} \right)
x ∼ N ( 0 , I n ) E [ d ( x , K ) ] ≤ n ( 1 − 5 1 2 α e 4 α 1 )
Proof: 注意到 ℓ 2 \ell_2 ℓ 2 1 1 1 E x ∼ N ( 0 , I n ) [ ∥ x ∥ 2 ] ≤ n \mathop{\mathbb E}\limits_{x\sim \mathcal N(0,I_n)}[\|x\|_2]\le\sqrt n x ∼ N ( 0 , I n ) E [ ∥ x ∥ 2 ] ≤ n Pr x ∼ N ( 0 , I n ) [ ∥ x ∥ 2 ≥ 4 α n ] ≤ e − 2 α n \Pr\limits_{x\sim \mathcal N(0,I_n)}[\|x\|_2\ge 4\sqrt{\alpha n}]\le \text e^{-2\alpha n} x ∼ N ( 0 , I n ) Pr [ ∥ x ∥ 2 ≥ 4 α n ] ≤ e − 2 α n
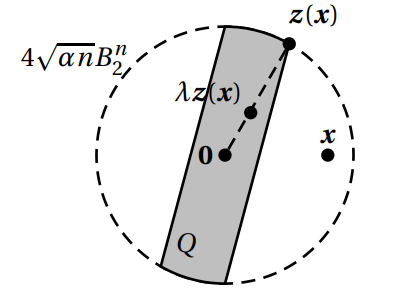
所以对于 Q ≜ K ∩ 4 α n B 2 n Q\triangleq K\cap 4\sqrt{\alpha n}B_2^n Q ≜ K ∩ 4 α n B 2 n n n n γ n ( Q ) ≥ γ n ( K ) − e − 2 α n ≥ e − 2 α n \gamma_n(Q)\ge \gamma_n(K)-\text e^{-2\alpha n}\ge \text e^{-2\alpha n} γ n ( Q ) ≥ γ n ( K ) − e − 2 α n ≥ e − 2 α n w ( Q ) ≥ n 2 e 2 α w(Q)\ge \dfrac{\sqrt n}{2\text e^{2\alpha}} w ( Q ) ≥ 2 e 2 α n
对于 x x x z ( x ) = argmax { ⟨ z , x ⟩ ∣ z ∈ Q } z(x)=\text{argmax}\{\langle z,x\rangle \mid z\in Q\} z ( x ) = argmax { ⟨ z , x ⟩ ∣ z ∈ Q }
w ( Q ) = E x ∼ N ( 0 , I n ) [ ⟨ z ( x ) , x / ∥ x ∥ 2 ⟩ ] ≥ n 2 e 2 α w(Q)=\mathop{\mathbb E}\limits_{x\sim \mathcal N(0,I_n)}[\langle z(x),x/\|x\|_2 \rangle]\ge \dfrac{\sqrt n}{2\text e^{2\alpha}}
w ( Q ) = x ∼ N ( 0 , I n ) E [ ⟨ z ( x ) , x / ∥ x ∥ 2 ⟩ ] ≥ 2 e 2 α n
设 λ ∈ [ 0 , 1 ] \lambda\in [0,1] λ ∈ [ 0 , 1 ] ∥ x − λ z ( x ) ∥ 2 \|x-\lambda z(x)\|_2 ∥ x − λ z ( x ) ∥ 2 λ \lambda λ
E x ∼ N ( 0 , I n ) [ ∥ x − λ z ( x ) ∥ 2 2 ] = E [ ∥ x ∥ 2 2 ] − 2 λ E [ ⟨ x , z ( x ) ⟩ ] + λ 2 E [ ∥ z ( x ) ∥ 2 2 ] = E [ ∥ x ∥ 2 2 ] − 2 λ E [ ∥ x ∥ 2 ] ⋅ E θ ∈ S n [ ⟨ θ , z ( θ ) ⟩ ] + λ 2 E [ ∥ z ( x ) ∥ 2 2 ] ≤ n − 2 λ ⋅ 1 2 n ⋅ n / ( 2 e 2 α ) + λ 2 ⋅ 16 α n \begin{aligned}
\mathop{\mathbb E}\limits_{x\sim N(0,I_n)}[\|x-\lambda z(x)\|_2^2] & =\mathbb E[\|x\|_2^2]-2\lambda\mathbb E[\langle x,z(x)\rangle]+\lambda^2\mathbb E[\|z(x)\|_2^2] \\
& =\mathbb E[\|x\|_2^2]-2\lambda\mathbb E[\|x\|_2]\cdot \mathop{\mathbb E}\limits_{\theta\in \mathbb S^n}[\langle \theta,z(\theta)\rangle]+\lambda^2\mathbb E[\|z(x)\|_2^2] \\
& \le n-2\lambda \cdot \dfrac 12\sqrt n\cdot \sqrt n/(2\text e^{2\alpha})+\lambda^2\cdot 16\alpha n
\end{aligned}
x ∼ N ( 0 , I n ) E [ ∥ x − λ z ( x ) ∥ 2 2 ] = E [ ∥ x ∥ 2 2 ] − 2 λ E [ ⟨ x , z ( x ) ⟩ ] + λ 2 E [ ∥ z ( x ) ∥ 2 2 ] = E [ ∥ x ∥ 2 2 ] − 2 λ E [ ∥ x ∥ 2 ] ⋅ θ ∈ S n E [ ⟨ θ , z ( θ ) ⟩ ] + λ 2 E [ ∥ z ( x ) ∥ 2 2 ] ≤ n − 2 λ ⋅ 2 1 n ⋅ n / ( 2 e 2 α ) + λ 2 ⋅ 1 6 α n
令 λ = 1 / ( 64 α e 2 α ) \lambda=1/(64\alpha\text e^{2\alpha}) λ = 1 / ( 6 4 α e 2 α )
E x ∼ N ( 0 , I n ) [ ∥ x − λ z ( x ) ∥ 2 2 ] ≤ n ( 1 − 1 256 e 4 α ) \mathop{\mathbb E}\limits_{x\sim N(0,I_n)}[\|x-\lambda z(x)\|_2^2]\le n\left(1-\dfrac 1{256\text e^{4\alpha}} \right)
x ∼ N ( 0 , I n ) E [ ∥ x − λ z ( x ) ∥ 2 2 ] ≤ n ( 1 − 2 5 6 e 4 α 1 )
所以:
E x ∼ N ( 0 , I n ) [ d ( x , K ) ] ≤ E x ∼ N ( 0 , I n ) [ ∥ x − λ z ( x ) ∥ 2 ] ≤ E [ ∥ x − λ z ( x ) ∥ 2 2 ] 1 / 2 ≤ n ⋅ 1 − 1 256 e 4 α ≤ n ( 1 − 1 512 e 2 α ) \mathop{\mathbb E}\limits_{x\sim \mathcal N(0,I_n)}[d(x,K)]\le \mathop{\mathbb E}\limits_{x\sim N(0,I_n)}[\|x-\lambda z(x)\|_2] \\
\le \mathbb E[\|x-\lambda z(x)\|_2^2]^{1/2}\le \sqrt n \cdot \sqrt{1-\dfrac{1}{256\text e^{4\alpha}}}\le \sqrt n\left(1-\dfrac{1}{512\text e^{2\alpha}}\right)
x ∼ N ( 0 , I n ) E [ d ( x , K ) ] ≤ x ∼ N ( 0 , I n ) E [ ∥ x − λ z ( x ) ∥ 2 ] ≤ E [ ∥ x − λ z ( x ) ∥ 2 2 ] 1 / 2 ≤ n ⋅ 1 − 2 5 6 e 4 α 1 ≤ n ( 1 − 5 1 2 e 2 α 1 )
期中第二个不等号用了 Jensen 不等式,最后一个不等号用了 Taylor 展开。□ \Box □
Lemma 6: 令 ϵ > 0 \epsilon>0 ϵ > 0 n n n
Pr x ∼ N ( 0 , I n ) [ d ( x , [ − ϵ , ϵ ] n ) ≥ ( 1 − 5 ϵ ) n ] ≥ 1 − exp ( − ϵ 2 n / 2 ) \Pr_{x\sim \mathcal N(0,I_n)}[d(x,[-\epsilon,\epsilon]^n)\ge (1-5\epsilon)\sqrt n]\ge 1-\exp(-\epsilon^2n/2)
x ∼ N ( 0 , I n ) Pr [ d ( x , [ − ϵ , ϵ ] n ) ≥ ( 1 − 5 ϵ ) n ] ≥ 1 − exp ( − ϵ 2 n / 2 )
Proof: 我们对 x x x x i ( i ∈ [ n ] ) x_i\ (i\in [n]) x i ( i ∈ [ n ] )
E [ d ( x i , [ − ϵ , ϵ ] ) 2 ] = E [ ( x i − y i ) 2 ] = E [ x i 2 ] − 2 E [ x i y i ] + E [ y i 2 ] ≥ 1 − 2 ϵ E [ ∣ x i ∣ ] = 1 − 2 ϵ 2 / π ≥ 1 − 2 ϵ \mathbb E[d(x_i,[-\epsilon,\epsilon])^2]=\mathbb E[(x_i-y_i)^2]=\mathbb E[x_i^2]-2\mathbb E[x_iy_i]+\mathbb E[y_i^2] \\
\ge 1-2\epsilon \mathbb E[|x_i|]=1-2\epsilon\sqrt{2/\pi}\ge 1-2\epsilon
E [ d ( x i , [ − ϵ , ϵ ] ) 2 ] = E [ ( x i − y i ) 2 ] = E [ x i 2 ] − 2 E [ x i y i ] + E [ y i 2 ] ≥ 1 − 2 ϵ E [ ∣ x i ∣ ] = 1 − 2 ϵ 2 / π ≥ 1 − 2 ϵ
再由 Lemma1 可知:
Pr [ F ( x ) < E [ F ( x ) ] − ϵ n ] ≤ exp ( − ϵ 2 n / 2 ) \Pr\left[ F(x)<\mathbb E[F(x)]-\epsilon\sqrt n \right]\le \exp(-\epsilon^2 n/2)
Pr [ F ( x ) < E [ F ( x ) ] − ϵ n ] ≤ exp ( − ϵ 2 n / 2 )
故得证。□ \Box □
有了这些技术引理的准备,我们可以开始证明主要定理。
我们先把上面介绍的算法再写一遍:
随机一个向量 x 0 ∼ N ( 0 , I n ) x_0\sim \mathcal N(0,I_n) x 0 ∼ N ( 0 , I n )
求解这样一个优化问题:x = argmin { ∥ x − x 0 ∥ 2 ∣ x ∈ K ∩ [ − ϵ , ϵ ] n } x=\text{argmin}\{\|x-x_0\|_2 \mid x\in K\cap [-\epsilon,\epsilon]^n\} x = argmin { ∥ x − x 0 ∥ 2 ∣ x ∈ K ∩ [ − ϵ , ϵ ] n }
输出 x x x
Proof of Thm: x 0 x_0 x 0 x ∗ x^* x ∗
E 1 ≜ “ d ( x 0 , [ − ϵ , ϵ ] n ) ≥ ( 1 − 5 ϵ ) n ” E 2 ≜ “ d ( x 0 , K ) ≤ ( 1 − 10 ϵ ) n , ∀ I ∈ [ n ] and ∣ I ∣ ≤ δ n ” \mathcal E_1\triangleq“d(x_0,[-\epsilon,\epsilon]^n)\ge (1-5\epsilon)\sqrt n” \\
\mathcal E_2\triangleq “d(x_0,K)\le (1-10\epsilon)\sqrt n,\ \forall I\in [n]\text{ and }|I|\le \delta n”
E 1 ≜ “ d ( x 0 , [ − ϵ , ϵ ] n ) ≥ ( 1 − 5 ϵ ) n ” E 2 ≜ “ d ( x 0 , K ) ≤ ( 1 − 1 0 ϵ ) n , ∀ I ∈ [ n ] and ∣ I ∣ ≤ δ n ”
由 Lemma 6 可知 Pr [ E 1 ] ≥ 1 − exp ( − ϵ 2 n / 2 ) \Pr[\mathcal E_1]\ge 1-\exp(-\epsilon^2 n/2) Pr [ E 1 ] ≥ 1 − exp ( − ϵ 2 n / 2 ) □ \Box □
实际上原文中主要定理的形式是更加一般的、它定义了对于一个子空间的高斯测度 γ H \gamma_H γ H [ − ϵ , ϵ ] n [-\epsilon,\epsilon]^n [ − ϵ , ϵ ] n [ − L , R ] ( L > 0 , R > 0 ) [-\bm L,\bm R]\ (\bm L>\bm 0,\bm R> \bm 0) [ − L , R ] ( L > 0 , R > 0 )
这个算法的主要好处就是对 α \alpha α α \alpha α α \alpha α
但这个算法不够快,这是因为要解的问题不是一个性质更好的线性规划问题。在论文 [ES18] 中,R. Eldan 和 M. Singh 提出了一个线性规划算法:
Thm: 对于任何常数 0 < ϵ < ( 1 − 2 / π 32 ) 4 0<\epsilon <\left(\dfrac{1-\sqrt{2/\pi}}{32}\right)^4 0 < ϵ < ( 3 2 1 − 2 / π ) 4 ϵ \epsilon ϵ δ \delta δ γ n ( K ) ≥ e − ϵ n \gamma_n(K)\ge \text e^{-\epsilon n} γ n ( K ) ≥ e − ϵ n K ⊆ R n K\subseteq \mathbb R^n K ⊆ R n x ∈ K ∩ [ − 1 , 1 ] n x\in K\cap [-1,1]^n x ∈ K ∩ [ − 1 , 1 ] n # { i ∈ [ n ] ∣ ∣ x i ∣ = 1 } ≥ δ n \#\{i\in [n]\mid |x_i|=1\}\ge \delta n # { i ∈ [ n ] ∣ ∣ x i ∣ = 1 } ≥ δ n 1 2 \dfrac 12 2 1
而算法如下:
随机一个向量 x 0 ∼ N ( 0 , I n ) x_0\sim \mathcal N(0,I_n) x 0 ∼ N ( 0 , I n )
求解这样一个优化问题:x = argmax { ⟨ x 0 , x ⟩ ∣ x ∈ K ∩ [ − 1 , 1 ] n } x=\text{argmax}\{\langle x_0,x \rangle \mid x\in K\cap [-1,1]^n\} x = argmax { ⟨ x 0 , x ⟩ ∣ x ∈ K ∩ [ − 1 , 1 ] n }
输出 x x x
但是从定理描述中也可以看到其对 ϵ \epsilon ϵ
[ES18] R. Eldan and M. Singh. Efficient algorithms for discrepancy minimization in convex sets. Random Struct. Algorithms , 53(2):289–307, 2018.
[Rot14] T. Rothvoß. Constructive discrepancy minimization for convex sets. In 55th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2014, Philadelphia, PA, USA, October 18-21, 2014 , pages 140–145, 2014.
[3] 王浩宇学长 2024/3/9 组会演讲