Approximation Algorithms for Maximum Cut

发表于 分类于

Improved Approximation Algorithms for Maximum Cut and Satisfiability Problems Using Semidefinite Programming (Michael X. Coemans and David P. Williamso, 1994) reading note.

Introduction

Defn (Maximum Cut Problem): Let G=(V,E,w)G=(V,E,w) be a undirected graph with weigh function w:E→Rw:E\to \mathbb R. One wants a subset SS of the vertex set VV such that the sum of the weights of the edges between SS and the complementary subset S‾\overline{S} is as large as possible.

The maximum cut problem can be written in the following integer programming form:

max⁡ 12∑i<j(1−xixj)wijs.t. xi∈{−1,1}, i=1,2,…,n(1)\begin{aligned} \max\ & \dfrac 12 \sum_{i<j}(1-x_ix_j)w_{ij} \\ \text{s.t. } & x_i\in \{-1,1\},\ i=1,2,\ldots,n \end{aligned} \tag{1}

However, maximum cut problem is a NP\textbf{NP}-complete problem, which means that it probably has no polynomial time algorithm.

Thus we try to find its approximate solution.

Relaxation

Since solving (1)(1) is NP\textbf{NP}-complete, we consider semidefinite relaxation of (1)(1).

xi∈{−1,1}=S1⟹vi∈Sn,x_i\in \{-1,1\}=\mathbb S^1\Longrightarrow v_i\in \mathbb S^n,

where Sk\mathbb S^k denotes the kk-dimensional unit sphere.

Then we can write down the semidefinite relaxation of (1)(1):

max⁡ 12∑i<j(1−Xij)wijs.t. vi∈Sn, i=1,2,…,nXij=⟨vi,vj⟩, i=1,2,…,n, j=1,2,…,n(2)\begin{aligned} \max\ & \dfrac 12 \sum_{i<j}(1-X_{ij})w_{ij} \\ \text{s.t. } & v_i\in \mathbb S^n,\ i=1,2,\ldots,n \\ & X_{ij}=\langle v_i,v_j \rangle,\ i=1,2,\ldots,n,\ j=1,2,\ldots,n \end{aligned} \tag{2}

Thm: XX is a semidefinite matrix. Thus problem (2)(2) is a semidefinite programming problem.

Proof: For every y∈Rny\in \mathbb R^n, we have: \vspace{-0.3cm}

yTXy=∑i,jyiyj⟨vi,vj⟩=∑i,j⟨yivi,yjvj⟩=⟨∑iyivi,∑iyivi⟩≥0,\begin{aligned} y^TXy & =\sum_{i,j} y_i y_j\langle v_i,v_j\rangle \\ & = \sum_{i,j} \langle y_i v_i,y_j v_j\rangle \\ & = \left\langle \sum_i y_iv_i,\sum_i y_iv_i\right\rangle\ge 0, \end{aligned}

as desired. □\Box

Algorithm

Then there is a simple randomized approximation algorithm for the maximum cut problem.

  • Solve (2)(2), obtaining an optimal set of vectors viv_i.
  • Let rr be a vector uniformly distributed on the unit sphere Sn\mathbb S^n.
  • Set S={i∣⟨vi,r⟩≥0}S = \{i\mid \langle v_i,r\rangle \ge 0 \}.

Remark: We can obtain {v1,…,vn}\{v_1,\ldots,v_n\} from XX by Cholesky decomposition, i.e. X=LTLX=L^TL and each column of LL is a viv_i.

Analysis

We analyze the approximate effect of the algorithm:

E[w(S,S‾)]≜E[Δ]=∑i<jwijPr⁡[sgn(⟨vi,r⟩)≠sgn(⟨vj,r⟩)]=∑i<jwij2arccos⁡(⟨vi,vj⟩)2π\begin{aligned} \mathbb E[w(S,\overline{S})]\triangleq\mathbb E[\Delta] & =\sum_{i<j} w_{ij}\Pr[\text{sgn}(\langle v_i,r\rangle)\ne \text{sgn}(\langle v_j,r\rangle)] \\ & =\sum_{i<j} w_{ij}\dfrac{2\arccos(\langle v_i,v_j\rangle)}{2\pi} \end{aligned}

Then let p∗p^\ast be the optimal value of problem (1)(1), and q∗q^\ast be the optimal value of problem (2)(2).

Since (2)(2) is a relaxation of (1)(1), we have that q∗≥p∗q^\ast\ge p^\ast. Thus the approximation ratio E[Δ]p∗≥E[Δ]q∗\dfrac{\mathbb E[\Delta]}{p^\ast}\ge \dfrac{\mathbb E[\Delta]}{q^\ast}.

If wij≥0w_{ij}\ge 0 for every i,ji,j, then we have:

E[Δ]q∗=2π⋅∑i<jwijarccos⁡(⟨vi,vj⟩)∑i<jwij(1−⟨vi,vj⟩)≥2πmin⁡i,jarccos⁡(⟨vi,vj⟩)1−⟨vi,vj⟩≥2πmin⁡θθ1−cos⁡(θ)≜α≈0.878…\begin{aligned} \dfrac{\mathbb E[\Delta]}{q^\ast} & =\dfrac 2\pi\cdot \dfrac{\sum_{i<j}w_{ij}\arccos(\langle v_i,v_j\rangle)}{\sum_{i<j}w_{ij}(1-\langle v_i,v_j\rangle)} \\ & \ge \dfrac 2\pi \min_{i,j}\dfrac{\arccos(\langle v_i,v_j\rangle)}{1-\langle v_i,v_j\rangle} \\ & \ge \dfrac 2\pi \min_{\theta}\dfrac{\theta}{1-\cos(\theta)}\triangleq \alpha\approx 0.878\ldots \end{aligned}

Remark: By using Markov inequality and the fact E[(p∗−Δ)/p∗]<0.122\mathbb E[(p^\ast-\Delta)/p^\ast]<0.122, we have:

Pr⁡[(p∗−Δ)/p∗>0.122ϵ]<E[(p∗−Δ)/p∗>0.122ϵ]1+ϵ<11+ϵ<1\Pr[(p^\ast-\Delta)/p^\ast>0.122\epsilon]<\dfrac{\mathbb E[(p^\ast-\Delta)/p^\ast>0.122\epsilon]}{1+\epsilon}<\dfrac 1{1+\epsilon}<1

We can repeat this algorithm many times to reduce the error probability.

Quality of the Relaxation

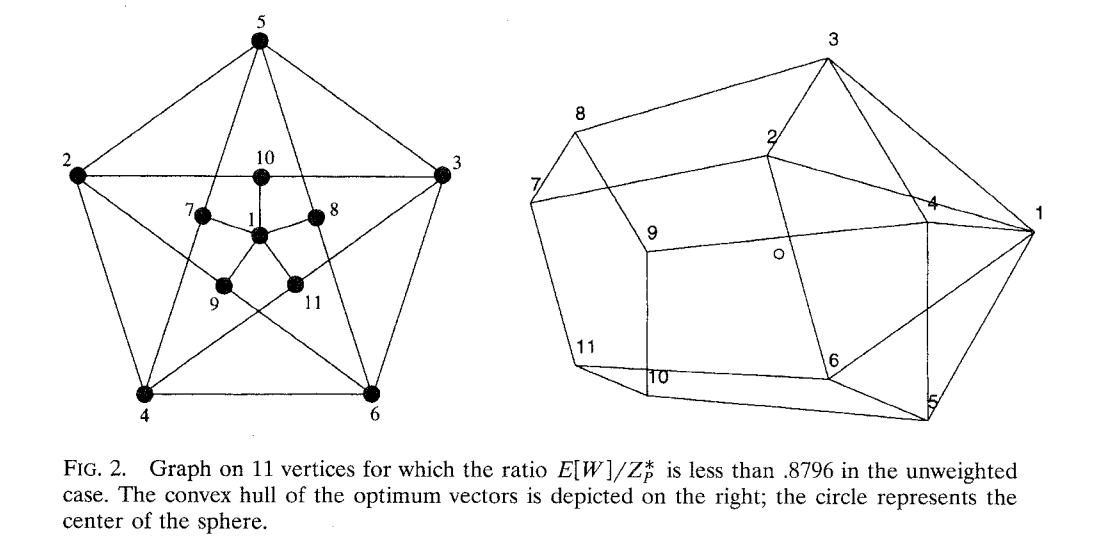
The following picture shows that the bound showed before is almostly tight.

pic1

Analysis for Negative Edge Weights

For negative edge weights, we have:

Thm: Let W−=∑i<jmin⁡{wij,0}W^-=\sum_{i<j}\min\{w_{ij},0\}. Then:

E[Δ]−W−≥α(q∗−W−)\mathbb E[\Delta]-W^-\ge \alpha\left(q^\ast-W^- \right)

The proof of this theorem is almostly the same as before.

Supplements

  • The maximum cut problem is APX\textbf{APX}-hard, meaning that there is no polynomial time approximation scheme, arbitrarily close to the optimal solution, for it, unless P=NP\textbf P = \textbf{NP}.
  • If the unique games conjecture is true, this is the best possible approximation ratio for maximum cut. (Subhash Khot, Guy Kindler, Elchanan Mossel and Ryan O’Donnell, 2004)

Thm (Unique Games Conjecture): Given any ϵ,δ>0\epsilon, \delta > 0, there exists some k>0k>0 depending on ϵ\epsilon and δ\delta, such that for the unique games problem with a universe of size kk, it is NP\textbf{NP}-hard to distinguish between instances in which at least a 1−ϵ1-\epsilon fraction of the constraints can be satisfied, and instances in which at most a δ\delta fraction of the constraints can be satisfied.

Further statements about UGC can be seen on https://www.zhihu.com/question/264803851

References

[1] Michel X. Goemans and David P. Williamson. 1995. “Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming.” J. ACM 42, 6 (Nov. 1995), 1115–1145.

[2] Lecture 3 of the course Algorithms for Big Data, 2024 spring, lecturer: Hu Ding and Qi Song.

[3] Subhash Khot, Guy Kindler, Elchanan Mossel and Ryan O’Donnell. “Optimal inapproximability results for MAX-CUT and other 2-variable CSPs?.” SIAM Journal on Computing 37.1 (2007): 319-357.